Our ASG runs for three months - February, August, and October, which constitute three stages of the group work. The activity of the ASG will be concluded with the workshop “Dissipative quantum chaos: from semi-groups to QED experiments”, held at PCS IBS on October 23 - 27, 2017.

Below are reports on the work of the group (updated once the corresponding stage is over).

February. This was the initiation of the group work. We figured out two problems, discussed and started to work on them. The problems are summarized into two corresponding questions:

•Can we see footprints of many-body localization in the asymptotic state of an open quantum system?

•Are there Floquet Lindbladians?

The first question is of interest in many different context and for many reasons, ranging from pure theoretical to experimental ones.  Assume we have a quantum system that exhibits many-body localization (MBL) phenomenon in the Hamiltonian limit [1]. Can we still see the MBL when the system is made open, i.e. it is subjected to dissipation? If it is possible then it would be a big deal: We will have (i) a unique state (not a set of eigenstates) which is, in addition, (ii) stable (with respect to perturbations), and (iii) will be able to control localization properties of this state. Very recent updates on the front of the MBL studies declared that the standard-like dephasing dissipation washes out the MBL, so that eventually an MBL system ends up in a maximally mixed state –independently of whether it was at the MBL phase or not in the Hamiltonian limit [2]. So, a specific non-trivial dissipation is the key prerequisite. This relates our studies to another ‘hot’ field, which is dissipative engineering of many-body states [3].

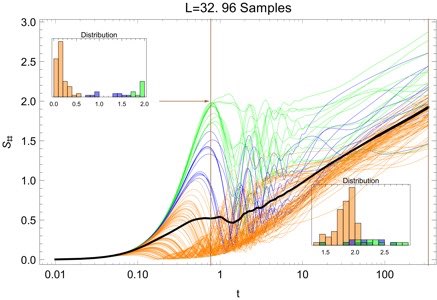
As for the members of the ASG, Mikahil Ivanchenko is involved (we will continue in August, when he comes with a PhD student, Igor Yuspiov). There are also members of the PCS are involved, that are Sergej Flach (who has a large expertise on disorder-induced localization phenomena and natural interest to many-body localization) and Ph. D. student Ihor Vakulchyk  (who has substantially advanced our numerical studies by bringing in the Matrix Product Operator (MPO) machinery [4] which allowed us to handle open quantum systems consisting up to ~50 spins; see figure below).

The second question is very interesting per se because this is a case when physical intuition (well, at least of most of the experts we have consulted) fails. Imagine that you have a quantum system that is periodically driven (in other words, the corresponding Hamiltonian is a time-periodic Hermitian operator) and, in addition, open. The dynamics of such system can be described with the Lindblad equation having a time-periodic generator on the rhs. Would it be possible to construct time-independent Lindblad generator (which we called “Floquet Lindladian”) yielding at stroboscopic instants of time – T, 2T, 3T, ... – the same states of the system as in the case of original time-dependent generator?

This is indeed possible when the system evolution is unitary, i.e., the dissipation is set to zero. Then the generator (now is in the rhs of the Schroedinger equation) is the Hermitian operator, the propagator over one period is its time-ordered exponent and, therefore, is a unitary operator. Thus, any branch of the logarithm of the latter could serve as a time-independent generator (also called “Floquet Hamiltonian” [5]). So the answer is always “yes” in the Hamiltonian limit.

It is not longer true when the system is open. This is because of the very specific structure of the Linblad equation [6]. In fact, as we demonstrate with a simple qubit model, Floquet Lindbladian does not exist in the most interesting case when the driving is neither diabatic nor adiabatic.

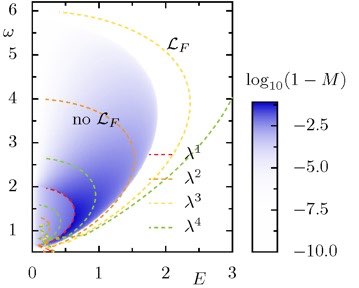
This direction is handled by a member of the ASG, André Eckardt, and his PhD student, Alexander Schnell (who performed all numerical simulations and thus visualized the answer; see figure below). We plan to continue along this direction and finalize those studies in a paper in October.

August.  We finalized our paper on the signatures of many-body localization  (MBL) in open quantum systems (see report for February for more information). It is on cond-mat now, https://arxiv.org/abs/1709.08882

Together with Dario Poletti and Michael Ivanchenko, we discussed the issue of time crystals in MBL systems, with the main focus on Floquet time crystals. The latter are systems that exhibit time-periodic oscillations (in term of some relevant observables) with a period being a multiple of the period of the driving (in most cases it is a period-doubling); in other words, such systems violate the discrete time translation symmetry imposed by the driving.

The key question was about introducing the dissipation in time-crystal systems in order to make them more ‘stable’ (hopefully) as clocks. We unfolded this question into the problem of time crystals in open systems, both classical (Markov continuous processes) and quantum ones. As it stands now (see recent works https://arxiv.org/abs/1708.09070 and https://arxiv.org/abs/1708.05014), time crystals are only possible in the thermodynamic limit, when the number of the system parts (spins, bosons, sites) goes to infinity. In this case, the appearance of time crystals corresponds to period doubling bifurcations in the corresponding non-linear mean-field equations. We think that it is indeed true for the classical open systems. However, it is not so in the quantum case: it is possible to have a perfect time crystal in a finite-size quantum system. We will continue in this direction in October.

[1] D.M. Basko, I.L. Aleiner, and B.L. Altshuler, Ann. Phys. 321, 1126 (2006).

[2] E. Levi, M. Heyl, I. Lesanovsky, JP. Garrahan, Phys. Rev. Lett.  116, 237203 (2016); M.H. Fischer, M. Maksymenko, and E. Altman, Phys. Rev. Lett. 116, 160401 (2016); see also recent experiment: Henrik P. Lüschen et al., Phys. Rev. X 7, 011034  (2017).

[3] S. Diehl, A. Micheli, A. Kantian, B. Kraus, H. P. Büchler, P. Zoller, Nature Physics 4, 878 (2008); F. Verstraete, M. M. Wolf, and J.I. Cirac, Nature Phys. 5, 633 (2009).

[4] M. Zwolak and G. Vidal, Phys. Rev. Lett. 93, 207205 (2004); R. Orús and G. Vidal, Phys. Rev. B 78, 155117 (2008).

[5] A. Eckardt, Rev. Mod. Phys. 89, 011004 (2017).

[6] R. Alicki and K. Lendi, Quantum Dynamical Semigroups and Applications (Lecture Notes in

Physics vol. 286, 1986).

October.  Two members of the group, Mikhail Ivanchenko and Igor Yusipov, finished and submitted a paper on quantum Lyapunov exponents (it is published now as a Rapid Communication in PRB [1]). Three others, Sergey Denisov, André Eckardt, and  Alexander Schnell, continued to work on their paper “Is there Floquet Lindbladian?” (see February’s report; it is on arxiv now [2]). There was a lot of discussions on the issue of Floquet time crystals in open quantum systems, with the whole group participating in them. The outcome was rather inconclusive but at the end the issue did not look so promising as it seamed at the beginning.

We had a great event in October, directly related to group’s work, that is International Workshop “Dissipative Quantum Chaos: from Semi-Groups to QED Experiments”, with a lot of relevant participants and talks.

Most important, there was a series of inspiring discussions with Karol Życzkowski, Dariusz Chruściński, Tomaž Prosen and Marko Žnidarič. Particularly, with Karol and Dariusz, we discussed a very interesting issue - “How to define and sample  random Lindbladians?”. These discussions (and initiated collaboration) resulted in a joint work  [3]. I consider it as one of the most valuable outcomes of the group work in October.

[1] I.I. Yusipov, T.V. Laptyeva, and M.V. Ivanchenko, Phys. Rev. B 97, 020301(R) (2018).

[2] A. Schnell, A. Eckardt, S. Denisov, Phys. Rev. B 101, 100301(R).

[3] S. Denisov, T. Laptyeva, W. Tarnowski, D. Chruściński, K. Życzkowski, https://arxiv.org/abs/1811.12282.

Final report.  In the retrospection, the work of the ASG is but a success. Most important, the agenda of the ASG “Dissipative Quantum Chaos” has been set (suffice it to say that group’s participants – now themselves, without the ASG convener – organized in 2019 another workshop on the subject – 708. WE Heraeus-Seminar “Quantization of dissipative chaos: ideas and means” in Bad Honnef, Germany).

Many collaborations were initiated in the IBS due to the ASG and the accompanying workshop. For example, it sparked the ongoing collaboration between K. Życzkowski, D. Chruściński, and S. Denisov (see a recent joint work [1]). The workshop has been noticed by the international community (the organizers got an invitation for a special issue in CHAOS from the editor-in-chief).

As for the scientific questions which were planned to address during the group activity, they were addressed thoroughly [1-5]. Even more, many other questions were discussed, new problems were formulated and new projects were launched. For example, a project on quasi-stationary states in open quantum systems, with participations of the PCS IBS researchers, was initiated [6].

As to formal quantifiers, the group work resulted (by now) in two published papers [2,3] (both are published as Rapid Communications in PRB) and three submitted papers [1,4,5] (with two of them are passing through second refereeing rounds in PRL [1,4]).

[1] S. Denisov, T. Laptyeva, W. Tarnowski, D. Chruściński, K. Życzkowski, https://arxiv.org/abs/1811.12282

[2] I.I. Yusipov, T.V. Laptyeva, and M.V. Ivanchenko, Phys. Rev. B 97, 020301(R) (2018).

[3] I. Vakulchyk, I. Yusipov, M. Ivanchenko, S. Flach, and S. Denisov, Phys. Rev. B 98, 020202(R) (2018).

[4] A. Schnell, A. Eckardt, and S. Denisov, https://arxiv.org/abs/1809.11121

[5] S. Denisov, T. Laptyeva, W. Tarnowski, D. Chruściński, K. Życzkowski, https://arxiv.org/abs/1811.12282

[6] I. Vakulchyk, M. Ivanchenko, S. Flach, and S.Denisov, Quasi-stationary states in open quantum systems, http://adsabs.harvard.edu/abs/2018APS..MARK26011V