5 April 2022 Tue 5 pm

< Previous

Topological phases and flat bands are important topics in condensed matter physics and photonics. In this talk I am going to introduce the topological phases and flat bands due to the particle nature of light, i.e., solely related to the quantized Fock states and the inhomogeneous coupling between them. In particular, we study a three-mode Jaynes-Cummings model, where three cavity modes are coupled to a two-level atom. The combinational Fock and atomic states form a two-dimensional honeycomb lattice (Fig.1), where the strain due to the inhomogeneity of the coupling strengths induces a Lifshitz topological phase transition between a semimetal and three band insulators within the lattice. In the semimetallic phase, the strain is equivalent to a pseudomagnetic field, which results in flat bands, i.e., pseudo Landau levels. We further construct a Haldane model where the topological phases can be characterized by the topological markers. This study demonstrates a fundamental distinction between the topological phases of bosons and fermions and provides a novel platform for studying topological physics in dimensions higher than three.

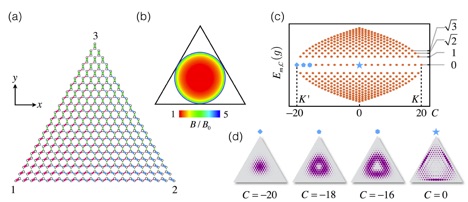
Figure 1: (a) The 2D Fock-state lattice with the line thickness proportional to the coupling strength. (b) The distribution of the pseudomagnetic field in the inner circle. Outside of the inner circle are band insulators. (c) The -scaling of the eigenenergies of the generalized Landau levels. (d) The wavefunction of the eigenstates.

[1] H Cai and DW Wang, National Science Review 8, nwaa196 (2021).

[2] J Yuan, H Cai, C Wu, SY Zhu, RB Liu and DW Wang, Phys. Rev. B 104, 035410 (2021).

[3] DW Wang, H Cai, RB Liu, and MO Scully, Phys. Rev. Lett. 116, 220502 (2016).

Next >